Lecture - 3 (jet strikes stationary vertical and inclined flat plate)

Jet strikes on vertical stationary flat plate

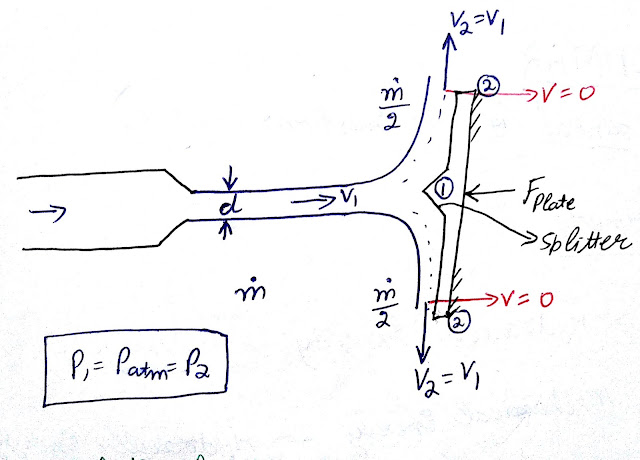
Let us consider a stationary vertical plate on which a jet is striking. The jet is having diameter 'd'. The mass flow rate of Jet is represented by 'm' kg/s. This simply means that 'm' kilogram of water is coming out of nozzle per second. The jet is striking at the middle of the plate with velocity 'V1' metre per second. After the impact of Jet on the plate, the jet will split equally and flows over the plate. After that the jet will exit the plate from its tip in tangential direction. Now here Jet is striking the plate normally or perpendicularly at point 1 and exit the plate tangentially from the tip of the vertical plate represented by point 2 with velocity 'V2' m/s. If we consider this plate to be frictionless then the entry velocity and exit velocity will be same (V1=V2). Also the pressure throughout the plate is atmospheric, wheather it will be on entry point of plate which is point 1 or it will be on exit point of plate which is point 2.
A splitter is made on the middle of the plate so that Jet will split properly and also to avoid any wear and tear of plate. Here half of mass flow rate will split in upward direction and rest half of mass flow rate will split in downward direction.

Now we have to study impact of jet or we can say force of jet on plate, in normal direction of plate and in tangential direction of plate. Here normal to plate is horizontal and tangential two plate is vertical direction.
Linear momentum of jet in horizontal or normal direction of plate at entry point which is point 1 = m*V1

Linear momentum of jet in vertical or tangential direction of plate at entry point Which is point1 = m*V1 = 0
Because, Here entry of Jet is only in normal direction or we can say in horizontal direction, so velocity of jet in tangential direction or vertical direction will be zero.

Linear momentum of jet in horizontal or normal direction of plate at above exit point which is point 2 = (m/2)*(V2) = 0
similarly linear momentum of jet in horizontal or normal direction of plate at below exit point 2 = (m/2)*(V2) = 0
Because, here exit of Jet will take place only in tangential direction of plate, therefore at both exit points velocity of jet in normal direction will be zero.

Linear momentum of jet in vertical or we can say a tangential direction of plate at above exit point Which is point2 = (m/2)*V2
Linear momentum of jet in vertical or tangential direction of plate at below exit point =  (m/2)*(-V2)
As we know half flow rate of water exit in upward direction and rest half flow rate of water exit in downward direction. So I am using sign convention because velocity is vector quantity. I am considering velocity with upward direction to be positive and velocity with downward direction to be negative.

Here cross-section area of jet(A) = (π/4)*(d*d)
and unit is square metre (m^2)

Discharge coming out of jet (Q) = A*V1
and unit is metre cube per second (m^3)/s

Mass flow rate of water (m) = ρ*A*V1
and unit is kilogram per second kg/s
'ρ' represents density of water


Now let us calculate force of jet in normal and tangential direction of plate.
'Fx ' represents force in horizontal direction
'Fn ' represents force in normal direction
'Fy ' represents force in vertical direction
'Ft ' represents force and tangential direction
'Fj ' represents force of jet

Fx = Fn = linear momentum of Jet at entry point 1 in horizontal direction - linear momentum of jet at exit point 2 in horizontal direction = mV1 - [(m/2)*V2 + (m/2)*(V2)]    ; As we know exit velocity of jet in horizontal or normal direction is zero
∴Fx = Fn = mV1 = ρ*A*V1*V1 newton

Fy = Ft = linear momentum of jet in vertical direction at entry point 1 - linear momentum of jet in vertical direction at exit point 2 = mV1 - [(m/2)*V2 + (m/2)*(-V2)]
Fy = Ft = m*0 - [0] = 0

Remember when Jet strikes flat plate then it will apply the force only in normal direction to plate only.
Therefore
Fx = Fn = Fj = mV1 = ρ*A*V1*V1 newton

Upto here Check this video illustration also Mechanical education hub 

Jet strikes a stationary incline plate

Here, our flat plate is inclind at an angle 'θ' with respect to axis of waterjet. All the notations which I used above will be same in this case also. The only difference is that the water Jet is not splitting into equal parts. 'm1' and 'Q1' are the mass flow rate and discharge at above exit point of plate and 'm2' and 'Q2' are the mass flow rate and discharge at below exit point of plate.

Here one more difference will be there which is because of inclination of plate and that is, the value of force in horizontal direction (Fx ) of plate will not be equal to value of force in normal direction (Fn ) of plate. Similarly value of force in vertical direction (Fy ) of plate will not be equal to value of force and tangential direction (Ft ) of plate.
Remember pressure throughout the process will remain constant that is atmospheric pressure.
P1 = P2 = Patm

m = m1 + m2
Q = Q1 + Q2
Let us consider a water Jet coming out of nozzle in horizontal axis strikes at inclined stationary plate at entry point 1 with mass flow rate 'm' and discharge 'Q'. Waterjet exit the plate from above and below exit point 2. By considering plate to be frictionless we can say that the velocity of jet at entry and exit will be equal (V1 = V2). Remember in the diagram only axis line of water Jet is shown, water jet will have its diameter 'd'.

Now we have to calculate forces in horizontal and vertical direction and also in normal and tangential direction of plate. We will do it by taking component of Forces. Let's draw the normal force component perpendicular to plate and tangential force component tangential to plate. Both the forces are shown in green colour.

Fn = linear momentum of Jet at entry point 1 in normal direction - linear momentum of jet at exit point 2 in normal direction = [m*V1*cos(90-θ)] - [(m1)*0 + (m2)*0] = m*V1*sinθ
 Fn = ρ*a*(V1^2)*sinθ

Remember in case of stationary plate force of water jet in tangential direction is always zero.
Ft = linear momentum of jet in tangential direction at entry point 1 - linear momentum of jet in tangential direction at exit point 2 = [m*V1*sin(90-θ)] - [(m1)*V2 + (m2)*(-V2)] = 0
ρ*Q*V1*cosθ - ρ*Q1*V2 + ρ*Q2*V2 = 0
Q*cosθ - Q1 + Q2 = 0

Now let us calculate the forces in horizontal and vertical direction. If we consider the below figure we can easily calculate force in horizontal and vertical direction. We just consider component of 'FN ' in horizontal and vertical direction.

Fx = FN cos(90-θ) = ρ*a*(V1^2)*{(sinθ)^2}
Fy = FN sin (90-θ) = ρ*a*(V1^2)*sinθ*cosθ

After this continue to lecture - 4