Lecture - 6 ( Newtonian, non Newtonian fluids and ideal fluids )

Newtonian fluids 

All those Fluids are known as newtonian Fluids for which shear stress (τ) is directly proportional to rate of shear strain (dθ/dt). 

τ ∝ dθ/dt 

τ = μ*(dθ/dt) or τ = μ*(du/dy) ; because from derivation in Lecture - 4 we know that dθ/dt = du/dy

Above equation is also termed as newton's law of viscosity. The relation of above equation is linear, where μ represent viscosity and is constant with respect to rate of shear strain. 

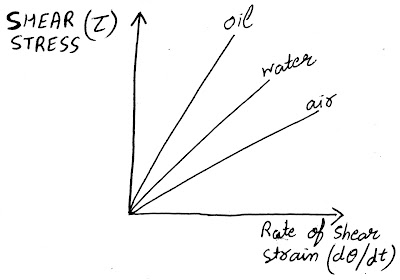
in the below figure graphical representation of different Newtonian fluids are shown- 

In above graph oil is having maximum slope because viscosity in oil is more and air is having minimum slope because viscosity of air is less, whereas water lies between oil and air because viscosity of water is less than oil but more than air.

A straight line passing through origin having constant slope is representing Newtonian fluids. Example are water, oil, mercury, air, petrol.

Non Newtonian fluids 

A non-Newtonian fluid is a fluif that does not follow Newton's law of viscosity, i.e. constant viscosity independent of stress. In non-Newtonian fluids, viscosity can change when under force to either more liquid or more solid. For example, ketchup becomes runnier when shaken and is thus a non-Newtonian fluid. The equation for non newtonian Fluids is 
τ = A*(du/dy)^n + B 
Here 'A' represents flow consistency index
'n' represents flow behaviour index
'B' represents yield shear stress
If in this equation when n=1 & B=0 then it became newtonian fluid. 
Let's study the different cases of non newtonian fluid 
Case 1 : VARIATION OF VISCOSITY (μ) WITH RESPECT TO RATE OF SHEAR STRESS (dθ/dt)

• Dilatant fluid - In dilatant fluids viscosity will increase with respect to rate of shear stress, therefore the slope of graph will be of increasing nature. Dilatant fluid are shear thickening fluid for example water and sugar solution. For these fluids value of flow behaviour Index (n) is positive and yield shear stress (B) is zero. Graph of dilatant fluid are shown in figure below

• Pseudo plastic fluids - In pseudo plastic fluids viscosity will decrease with respect to rate of shear stress, therefore the slope of graph will be of decreasing nature. Pseudoplastic fluid are shear thinning fluid for example paint, blood, lipstick. For these Fluids value of flow behaviour index (n) is negative and yield shear stress (B) is zero. Graph of pseudoplastic fluid is shown in figure below

• Bingham fluids - in bingham fluids slope of craft will remain constant but the line of graph will not intersect the origin point. Here flow behaviour index (n) is equal to 1 and yield shear stress (B) will not be equal to zero. Examples for toothpaste and gel. Graph of bingham fluid is shown in figure below 

Case 2 : VARIATION OF VISCOSITY (μ) WITH RESPECT TO TIME

• Rheopectic fluids - In Rheopectic fluids viscosity will increase with respect to time. For these Fluids value of flow behaviour index (n) is positive and yield shear stress (B) is not equal to zero. Graph of rheopectic Fluids is shown in figure below

            

• Thixotropic fluids - In thixotropic fluids viscosity will decrease with respect to time. For these fluids value of flow behaviour index (n) is negative and yield shear stress (B) is not equal to zero. Graph of thixotropic fluids is shown in figure below

     

Overall conclusion of all types of Fluids discuss above is shown in one τ vs dθ/dt graph which is as follows

Ideal fluids

These are hypothetical fluids whose viscosity is zero and the resulting motion we get is ideal or inviscid flow. in an ideal fluid there is no existence of shear force because of vanishing viscosity. These are incompressible fluids. Because of absence of viscosity there is no Cohesive forces in the fluid therefore surface tension ideal fluid is also zero.